-
The characteristic equation of a closed-loop system is s(s + 1)(s + 3) + k(s + 2) = 0, k > 0. Which of the following statements is true?
-
- Its roots are always real
- It cannot have a breakaway point in the range – 1 < Re[s] < 0
- Two of its roots tend to infinity along the asymptotes Re[s] = – 1
- It may have complex roots in the right half plane
Correct Option: C
Given : s(s + 1) (s + 3) + k(s + 2) = 0; k > 0
| ⇒ 1 + | = 0 | |
| s(s + 1)(s + 3) |
But 1 + G(s) H(s) = 0
| ∴ G(s) H(s ) = | ||
| s(s + 1)(s + 3) |
Roots s = 0, s = – 1, s = – 3 (poles); s = – 2 (zero)
It has real pole or zeros.
| φA = | × 180° | |
| n - m |
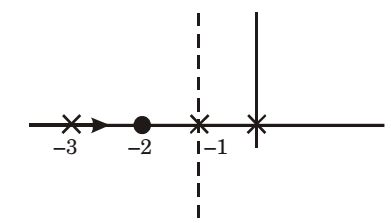
At s = 0, Asymptotes
| φ0 = | = 90° | |
| 2 |
| At s = 1, φ1 = | = 270° | |
| 2 |
Centroid,
| (-σA) = | ||
| number of poles - number of zeros |
∴ Re[s] = – 1

