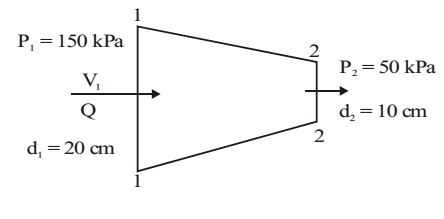
Consider steady, incompressible and irrotational flow through

Home » Fluid Mechanics and Hydraulic Machinery » Fluid Mechanics and Hydraulic Machinery Miscellaneous » Question

Consider steady, incompressible and irrotational flow through a reducer in a horizontal pipe where the diameter is reduced from 20 cm to 10 cm. The pressure in the 20 cm pipe just upstream of the reducer is 150 kPa. The fluid has a vapour pressure of 50 kPa and a specific weight of 5 kN / m³ . Neglecting frictional effects, the maximum discharge (in m³ / s) that can pass through the reducer without causing cavitation is

1. 0.05
2. 0.16
3. 0.27
4. 0.38

Correct Option: B

Considering potential head difference = 0,
i.e z₁ = z₂
Apply Bernoulli’s theorem

	p	+	v²	= C
	ρg		2g

	p₁	+	v₁²	=	p₂	+	v₂²
	w₁		2g		w₂		2g

But w₁ = w₂ = w = 5 (incompressible flow)

∴	150	+	v₁²	=	50	+	v₂²
	5		2g		5		2g

or	v₂² - v₁²	=	150 - 50
	2g		5

or	v₂² - v₁²	= 20 m ....(1)
	2g

Also, discharge, Q =		π	d₁²		v₁ =		π	d₂²		v₂
		4					4

or	v₁	=		d₂		²	=		10		²
	v₂			d₁					20

or v₁ =	v₂	......(2)
	4

From equations (1) and (2)

		v₂² -	v₂²
			16		= 20

		2g

or	15v₂²	= 20
	32g

or v₂ = √(20 × 32g) / 15 = 20.45 m /s

∴ Discharge , Q =		π	d₂²		v₂
		4

=	π	(0.1)² × 20.45 = 0.16 m³ /sec
	4