A closed cylinder having a radius R and height H is filled

A closed cylinder having a radius R and height H is filled with oil of density ρ. If the cylinder is rotated about its axis at an angular velocity of ω, the thrust at the bottom of the cylinder is

We know that

	δp	=	ρv²	=	ρ.ω²r²	= δω²r
	δr		r		r

[∵ v = ω × r]

	^p	δp =		^r	ρω²r dr
	₀			₀

p =	ρ	ω²r²
	2

Area of circular ring = 2πrdr
Force on elementry ring
= Intensity of pressure × Area of ring

=	ρ	ω²r²2πr dr
	2

∴ Total force on the top of the cylinder

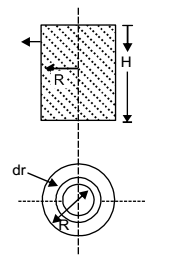
=		^R	ρ	ρω²r²2π r dr
		₀	2

=	ρ	ρω²r²2π		^R	r³ dr
	2			₀

	ρ	. ω²2π	R²	=	ρ	ω² × πR⁴
	2		4		4

Thrust at the bottom of the cylinder
= Weight of water in cylinder + Total force on the top of cylinder

= ρg × πR² × H +	ρ	ω² × πR⁴
	4

= πR²		ρω²R²	+ ρgH
		4

πR²		ρ ω²R²	+ ρ gH
		4