-
A wire of length 340 mm is to be cut into two parts. One of the parts is to be made into a square and the other into a rectangle where sides are in the ratio of 1 :2. What is the length of the side of the square (in mm) such that the combined area of the square and the rectangle is a MINIMUM?
-
- 30
- 40
- 120
- 180
Correct Option: B
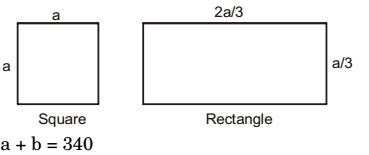
| Perimeter of rectangle = 2 |  | + |  | = 2a | ||
| 3 | 3 |
| Length of square = | ||
| 4 |
| Total area = |  |  | ² | + | = f'(a) | ||
| 4 | 4 |
Condition for minimum area f'(a) = 0
| 2 |  |  |  |  | + | a = 0 | |||
| 4 | 2 | 9 |
| a = | (340 - 20) | |||
| 9 | 4 |
a = 90
| Length of the square = | = 40 mm | |
| 4 |

