-
In figure given below
m(t) = 2 sin 2πt t s(t) = cos 200 πt and n(t) = sin 199 πt . The output y(t) t 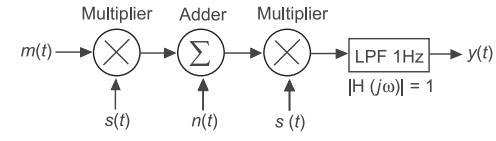
-
-
sin 2πt 2t -
sin 2πt + sin πt cos 3πt 2t t -
sin 2πt + sin 0.5πt cos 1.5πt 2t t -
sin 2πt + sin πt cos 0.75πt 2t t
-
Correct Option: C
m(t) s(t) = y1(t)
=
| = | |
| t |
or
| y1(t) = | |
| t |
y2(t) = y1(t) + n(t)
| = | + | ||
| t | t |
Now y(t) = y2(t).s(t)
| = | |
| t |
or
| y(t) = | [sin (402πt) + sin(2πt) − {sin(389πt) − sin2πt} + sin(399πt) − sin(πt)] | |
| 2t |
After filtering equation (C) through LPF with cut-off frequency 1 Hz we get
or
| y(t) = | |
| 2t |
or
| y(t) = | |
| 2t |
or
| y(t) = | + | cos 1.5πt | ||
| 2t | t |
Hence alternative (C) is the correct choice.

