-
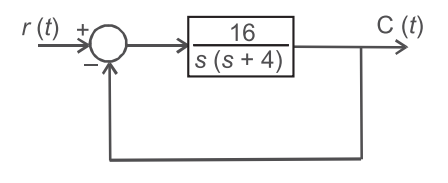
In the system shown in given figure, r(t) = sin ωt. The steady-state response C (t) will exhibit a resonance peak at a frequency of—
-
- 4 rad/sec
- 1/ 2√⎯ 2 rad/sec
- 2 rad/sec
- 2⎯√2rad/sec
- 4 rad/sec
Correct Option: D
From given figure
| C(s) | = | 16/(s+4)s |
| R(s) | 1 + 16/(s + 4) × 1/s |
| C(s) | = | |
| R(s) | 16 + s(s + 4) |
or,
| C(jω) | = | = | ||
| R(jω) | 16 + jω (jω + 4) | (16 - ω2 + j4ω) |
| tan-1 |  |  | ||
| √(16 - ω2)2 | 16 - ω |
for resonance to occur.
| d | f(ω) = | d | [(16 – ω2)2 + (4ω)2] | = 0 |
| dω | dω |
4ω2 – 32ω = 0
ω = √8 =2√2