-
Which one of the following is TRUE ?
-
- The language L = {anbn | ≥ 0} is regular.
- The language L = {an | n is prime} is regular.
- The language L = {w | w has 3k + 1b's for some k ∈ N with ∑ = {a, b}} is regular.
- The language L = {ww | w ∈ ∑* with ∑ = {0, 1}} is regular.
- The language L = {anbn | ≥ 0} is regular.
Correct Option: C
We know that a language L is regular if an equivalent finite Automata can be constructed for it. DFA can be constructed for L as follows :
Note that L contains the strings that has 3k + 1 number of b 's (that is 4, 7, 10, .......n ...... no. of b 's and any no. of a 's)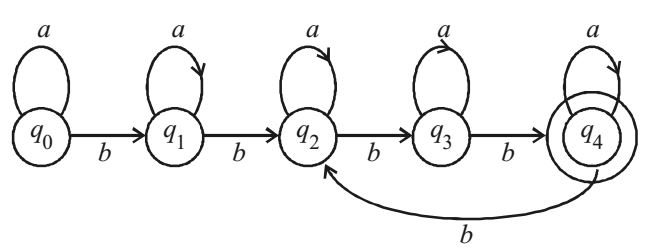
q0 is the initial state. q4 is the final state.
FA state remains same when input symbol is " a " at any point of time.
When 1st ' b ' is read, state is changed from q0 to q1.
When 2nd ' b ' is read, state is changed from q1 to q2.
When 3rd ' b ' is read, state is changed from q2 to q3.
When 4th ' b ' is read, state is changed from q3 to q4.
If no more ' b ' is encountered, the string is accepted when last input symbol is read.
However if 5th " b " is there is string, state is changed from q1 to q2 so that to accept the string 2 more bs must be there in the string at least.
Continuing in this way only those strings are accepted that has 3k + 1 ( k ∈ N ) number of b's. (i.e. 4, 7, 10... number of b's).

