Correct Option: C

The number of elements that can be sorted in Θ (log n) time using heap

sort is Θ		log n
		log logn

Consider the number of elements is "k", which can be sorted in θ (k log k) time. Analyzing the options in decreasing order of complexity since we need a tight bound i.e., θ.

i.e., θ (log n) , Θ		log n		, Θ(√log n) , Θ(1)
		log logn

So if k ∈ Θ (log n) time required for heap sort is O (k log k) i.e.,
θ (log n × log log n), But this is not in Θ (log n)

If k ∈ Θ		log n		time required for Heap Sort
		log logn

Θ		log n	× log		log n
		log logn			log logn

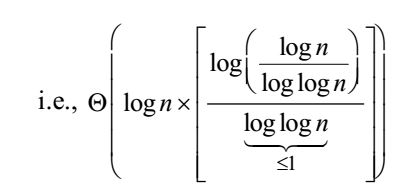
So, this is in Θ (log n)

Hence , answer is (c) Θ		log n
		log logn