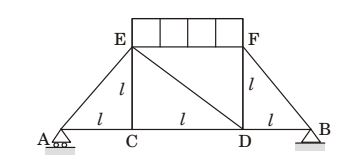
A truss consists of horizontal members (AC, CD, DB and EF)

A truss consists of horizontal members (AC, CD, DB and EF) and vertical members (CE and DF) having length l each. The-members AE, DE and BF are inclined at 45° to the horizontal For the uniformly distributed load p per unit length on the members EF of the truss shown in figure given below, the force in the member CD is

Total load on EF member = pl
where l = length of EF
For horizontal equilibrium R_A + R_B = Pl

Taking moment about A, we have

pl ×	3l	= R_B × 3l
	2

⇒ R_B =	Pl
	2

Considering a point A.
For horizontal equilibrium F_AC + F_AE cos 45° = 0

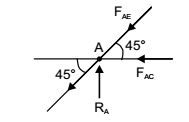
For vertical equilibrium R_A – F_AE sin 45° = 0

⇒ F_AE =	R_A	=	Pl	=	Pl
	sin 45°		2 × (1 / √2)		√2

∴ F_AC = -F_AE cos45° =	-Pl	.	1	=	-Pl
	√2		√2		2

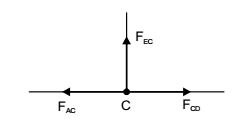
–ve sign shows that the force on member AC is opposite of assumed. Now considering a point C For horizontal equilibrium

F_AC = F_CD =	Pl
	2

	2pl
	3