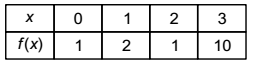
The values of a function f(x) are tabulated below: Using

The values of a function f(x) are tabulated below:

Using Newton's forward difference formula, the cubic polynomial that can be fitted to the above data, is

1. 2x³ + 7x² – 6x + 2
2. 2x³ - 7x² + 6x – 2
3. x³ – 7x² – 6x² + 1
4. 2x³ - 7x² + 6x + 1

Difference table as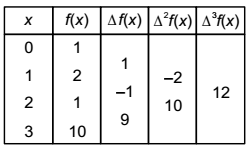

We take x₀ = 0, p =	x - 0	= x [∵ k = 1]
	k

using Newton’s forward interpolation formulae, we get

f(x) = f(0) +		x	Δ f(0) +	x(x-1)
		1		1.2

∆²f(0) +	x(x-1)(x-2)	∆³f(0)
	1.2.3

= 1 + x(1) +		x(x-1)	(-2) +	x(x-1)(x-2)	(12)
		2		6

= 1 + x + (x – x²) + 2x(x² – 3x + 2)
= 1 + x + x – x² + 2x³ – 6x + 4x
= 2x³ – 7x² + 6x + 1