-
A point mass is shot vertically up from ground level with a velocity of 4 m/s at time, t = 0. It loses 20% of its impact velocity after each collision with the ground. Assuming that the acceleration due to gravity is 10 m/s2 and that air resistance is negligible, the mass stops bouncing and comes to complete rest on the ground after a total time (in seconds) of
-
- 1
- 2
- 4
- ∞
Correct Option: C
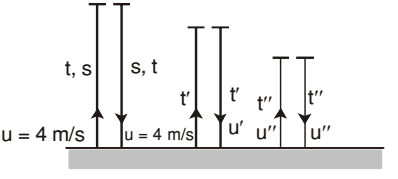
(1) → t =?
v = u + at
0 = 4 – 10t
| t = | = 0.4s | 10 |
(2) → t' =?
u' = 0.8 × u = 0.8 × 4 = 3.2 m/s
v' = u' + at'
0 = 3.2 – 10t'
| t' = | = 0.32s | 10 |
(3) → t'' =?
u'' = 0.8 u' = 0.8 × 3.2 = 2.56 m/s
v'' = u'' + at''
0 = 2.56 – 10t''
t'' = 0.256s
So, t, t', t'' are forming a GP series
So, total time = 2(t + t' + t'' +.... 0)
= 2[0.4 + 0.32 + 0.256 + ....0] = 2 × 2 = 4 seconds

