-
Two isotropic antennas are separated by a distance of two wavelength if both the antennas are fed with currents of equal phase and magnitude. The number of lobes in the radiation pattern in the horizontal plane are—
-
- 2
- 4
- 6
- 8
Correct Option: A
Since both are fed with currents of equal phase and magnitude so we get from the synopsis the relation of radiation pattern with separation d, having same phase and magnitude
| Enor = cos |  | cos θ |  | |
| 2 |
where,
| β = | , d = 2λ | |
| λ |
| Enor = cos |  | cos θ |  | = cos (2π cos θ) | ||
| λ | 2 |
for maxima Enor = ± 1
cos (2 π cos θ) = ± 1
∴ 2 π cos π = ± nπ
when n = 0, 1, 2....
or
| 2 cos θ = ± | |
| 2 |
| θ = cos −1 |  | ± |  | |
| 2 |
Values of θ may be for n = 0, 1, 2
| n = 0, | = 0 | |
| 2 |
| n = 1 ± | = ± | ; | ||
| 2 | 2 |
θ = 60º, 240º, 120º
| n = 1 ± | = ± 1; | |
| 2 |
θ = 0º, 180º
for minima values,we have
cos (2 π cos θ)=0
| 2 π cos θ = ± (2n + 1) | |
| 2 |
where n = 0, 1, 2, .....
| cos θ = ± | |
| 4 |
| for n = 0,cos θ = ± | given θ = 75.5°,255.5° | |
| 4 |
| n = 1,cos θ = ± | given θ = 41.4°,221.4° | |
| 4 |
| n = 2,cos θ = ± | (which is not valid) | |
| 4 |
so lobes are maxima at
0º, 60º, 180º, 240º, 120º, 310º
minima at
41.4º, 75.5º, 221.4º, 255.5º, 104.5º, 138.5º
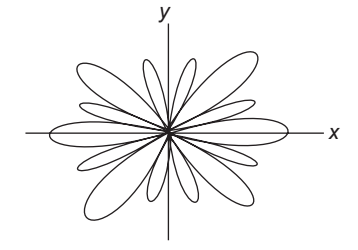
so we see from the above that in horizontal plane there are two maxima at 0º and 180º.

