-
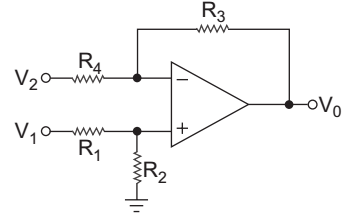
For the circuit given below CMRR is given by:
-
-
1 
R3(R1 + R2) + R2(R4 + R3) 
2 R3(R1 + R2) - R1(R4 + R3) -
1 
R3(R1 + R2) - R2(R4 + R3) 
2 R3(R1 + R2) + R1(R4 + R3) -
1 
R3(R1 + R2) - R2(R4 + R3) 
2 R3(R1 + R2) - R1(R4 + R3) -
1 
R3(R1 + R2) + R2(R4 + R3) 
2 R3(R1 + R2) + R1(R4 + R3)
-
Correct Option: A
| VB = Vi |  |  | ||
| R1 + R2 |
By using superposition principle.
| Vo = – | . V2 + VB. |  | 1 + |  | |||
| R4 | R4 |
| or Vo = – | . V2 + V1. |  |  | · |  |  | ............(i) | |||
| R4 | R1 + R2 | R4 |
we know,
| Vc = | .............(ii) | |
| 2 |
Vd = V1 – V2 …(iii)
from equations (ii) and (iii)
| V1 = Vc + | .............(iv) | |
| 2 |
| V2 = Vc – | .............(v) | |
| 2 |
Substituting these values in equation (i)
| Vo = – |  | Vc – |  | + |  | Vc + |  |  |  | + |  |  | |||||
| R4 | 2 | 2 | R1 + R2 | R4 |
| or Vo = Vc |  |  | · |  |  | - | + |  |  |  |  | ...........(vi) | ||||||||
| R1 + R2 | R4 | R4 | 2 | R1 + R2 | R4 | R4 |
| Since, CMRR = | ||
| AcM |
| where AdM = | |Vd = 0 so from equation (vi) | |
| Vd |
| AdM | = |  |  |  |  | + | |||||
| Vd | 2 | R1 + R2 | R4 | R4 |
| and AdM = | |Vd = 0 | |
| Vd |
| AdM = |  |  |  |  | - | |||
| R1 + R2 | R4 | R4 |
finally
| CMRR = |  |  | ||
| 2 | R3(R1 + R2) - R1(R4 + R3) |
Hence alternative (A) is the correct choice.

