Given Vc = e– 2t (sin t + cos t) the value of VL is given

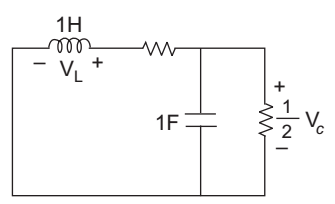
Home » Network Theory » Network Elements and the Concept of Circuit » Question

Given V_c = e– 2t (sin t + cos t) the value of V_L is given by—

1. – e^{– 2t} sin t + 3e^–2t cos t
2. – e^{– 2t} sin t + e^–2t cos t
3. e^–2t sin t – 3 e^–2t cos t
4. 5 e^{– 2t} (sin t – cos t)

Correct Option: C

V_C = e^{– 2t} (sin t + cos t)
I _R = V_C 1/2 = 2^{e^{– 2t}} (sin t + cos t) amp

I _C = C d dt V_C = 1. d dt e^{– 2t} (sin t + cos t)
= e^{– 2t} d dt sin t + sin t d dt e^{– 2t} + e^{– 2t}
d dt cos t + cos t d dt e^{– 2t}
= e^{– 2t} (cos t – sin t) + sin t (– 2) e^{– 2t} + cos t (–2) e^{– 2t}
= e^{– 2t} [cos t – sin t – 2 sin t – 2 cos t]
= e^{– 2t} [– cos t – 3 sin t] amp
so I_L = I_C + I_R = e^{– 2t} (– cos t – 3 sin t) + 2e^{– 2t} (sin t + cos t)
I _L = I_C + I_R = e^{– 2t} (– cos t – 3 sin t) + 2e^{– 2t} (sin t + cos t)
V_L = L d dt I_L = 1. d dt e^{– 2t} (cos t – sin t)
or V_L = (cos t – sin t) d dt e^{– 2t} + e^{– 2t} d dt (cos t – sin t)
or V_L = (cos t – sin t) (– 2) e^{– 2t} + e^{– 2t} (– sin t – cos t)
or V_L = e^{– 2t} (sin t – 3 cos t)
or V_L = e^{– 2t} sin t – 3 e^{– 2t} cos t volt.