-
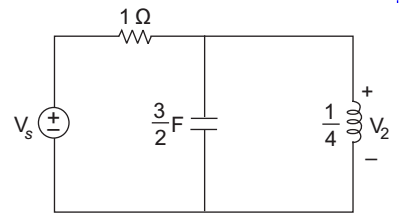
Given V2 = 2 cos 2t = 2 0°, the value of Vs is given by—
-
- 3 0°
- 29 tan– 1 2.5
- 104 tan– 1 5
- 2 2 45°
Correct Option: D
Given that
V2 = 2 cos 2 t = 2 ∠ 0° 
| I L (s) = | = | 1s / 4 | s |
| I C (s) = | = | 1 / (3s / 2) | 2 |
Total current flowing through
1 Ω = IL (s) + IC (s)
| V 2 = |  | + |  | s | 2 |
| = V2 |  | 8 + 3s2 |  | |
| 2s |
Voltage drop across across resistance
| = 1. V2 |  | 8 + 3j 2 × ω2 |  | |
| 2j × 2 |
On comparing with
V2 = 2 cos 2t = 2 ∠ 0º
Here, = ω = 2
| = 1. V2 |  | 8 – 3 × 4 |  | |
| 2j × 2 |
Voltage drop across 1 Ω resistance
= V2 = V2 ∠ 90°
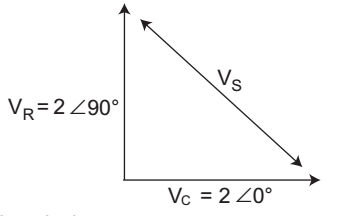
By using triangle law VS = 2√2 ∠ 45°

