-
Switch S is in position (1) for a long time at t = 0 comes to position (2). Find i L (t)—
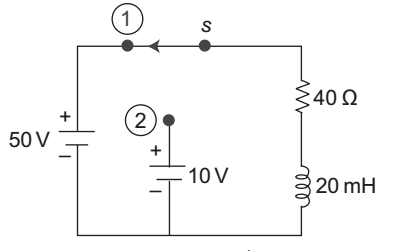
-
- i (t) = (1.25 – 0.25) e – t / 5 × 103 + .25
- i (t) = (1.25 – 0.25) e – t / 5 × 10–3 + .25
- i (t) = (.25 – 1.25) e – t / 0.5 × 10–3 + .5
- i (t) = (.25 – .25) e – t / 0.5 × 10–3 + .5
Correct Option: B
It may be noted that in this problem differential approach becomes complex. So we will apply here general approach.
We know that
i (t)=[i (0) – i (∞)] e –t / τ + i (∞) .....(i)
| here i (0–) = i (0+) = | = 1.25 amp. | 40 |
| i (∞) = | = .25 | 40 |
| τ = | = | = .5 × 10–3 | R | 40 |
so on putting these values in equation (i), we get
i L (t) = (1.25 – 0.25) e –1 5 × 10–3 + .25

