-
The power delivered by the dependent source—
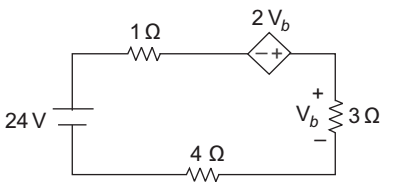
-
- 864 W
- – 864 W
- 288 W
- – 288 W
Correct Option: A
Let the current I is flowing through the circuit. Apply KVL to the loop 
24 – i.1 + 2Vb + 3i – 4i = 0
24 = 8i – 2Vb (∵ Vb = 3i)
24 = 81 – 2 × 3i = 8i – 6i
24 = 2i
i = 12 amp.
In order to calculate the power delivered by the dependent source put all the power dissipated across the resistance equal to power declined by the different dependent and independent sources. Power delivered by the sources = power dissipated across the resistor Power delivered by the dependent source
+ 24 × i = i 2 × 3 + i 2 × 4 + i 2 × 1
or Power delivered by the dependent source = i 2 8 – 24 i = (12)2 × 8 – 24 × 12
= 144 × 8 – 288 = 864 watts

